Revista Argentina de Humanidades y Ciencias Sociales
ISSN 1669-1555

Volumen 11, nº 2 (2013)

Estudiante avanzado de la Licenciatura en Antropología Social de la Facultad de Ciencias Sociales, Universidad Nacional del Centro de la Provincia de Buenos Aires (sede Olavarría)

El presente trabajo fue elaborado a partir de los resultados obtenidos en el estudio titulado “Ciencia en y fuera de las escuelas. Sentidos y prácticas científicas en estudiantes de nivel medio”, llevado a cabo a partir de una beca “Estímulo a las Vocaciones Científicas 2012” del CIN. En este artículo se busca dar cuenta de los procesos de apropiación del conocimiento científico en espacios escolares; tomando a las clases que se desarrollan en el aula y los talleres orientados a la preparación de los estudiantes para las olimpíadas como los dos ámbitos privilegiados de observación y análisis. Se pretende, por otro lado, relacionar dichos procesos con las concepciones de ciencia que sostienen los alumnos del establecimiento en el que se llevó a cabo toda la investigación. El trabajo de campo etnográfico fue realizado en una escuela de educación media nacional dependiente de una universidad pública.

This paper was prepared from the results of the study entitled “Science in and out of school. Meanings and scientific practices of students in the middle level of teaching”, supported by a research grant “Estímulo a las Vocaciones Científicas 2012” of CIN. This article shows the processes of appropriation of scientific knowledge that are developed in different school contexts; observing classes taking place in the classroom and workshops aimed at preparing students for school competitions. It pretends to connect the mentioned processes with the representations about scientific knowledge of institution’s students. The ethnographic fieldwork was done in a middle level school dependent on a public university.

Key words

El presente trabajo fue elaborado a partir de los resultados obtenidos en el estudio titulado “Ciencia en y fuera de las escuelas. Sentidos y prácticas científicas en estudiantes de nivel medio” (dirigido y codirigido por la Dr. Dora Luján Coria y el Mg. Gastón O. Marmissolle), llevado a cabo a partir de una beca “Estímulo a las Vocaciones Científicas 2012” del CIN. Las actividades de investigación necesarias para cumplir con dicho plan se inscriben en el Proyecto Estudios en Comunicación y Cultura en Olavarría (ECCO), radicado en la Facultad de Ciencias Sociales - Universidad Nacional del Centro de la Provincia de Buenos Aires.

En este artículo se busca dar cuenta de los procesos de apropiación del conocimiento científico en espacios escolares; tomando a las clases que se desarrollan en el aula y los talleres orientados a la preparación de los estudiantes para las olimpíadas como los dos ámbitos privilegiados de observación y análisis. Se pretende, por otro lado, relacionar dichos procesos con las concepciones de ciencia que sostienen los alumnos del establecimiento en el que se llevó a cabo toda la investigación.

El trabajo de campo adoptó un enfoque etnográfico, entendiendo como tal “(…) una concepción y práctica de conocimiento que busca comprender los fenómenos sociales desde la perspectiva de sus miembros” (Guber; 2001:11-12). La relevancia de la etnografía en este tipo de estudios se refiere al hecho que “(…) adoptar un enfoque etnográfico es elaborar una representación coherente de lo que piensan y dicen los nativos, de modo que esa ‘descripción’ no es ni el mundo de los nativos, ni cómo el mundo es para ellos, sino una conclusión interpretativa que elabora el investigador (…). Pero a diferencia de otros informes, esa conclusión proviene de la articulación entre la elaboración teórica del investigador y su contacto prolongado con los nativos” (Guber; 2001:15).

Por otro parte, en el proceso de una investigación etnográfica, la observación participante adquiere un lugar de central. Debido a la posibilidad de acceder a las situaciones bajo estudio en toda su complejidad y en las instancias en las que éstas se desarrollan, y a la oportunidad de acercarse a la perspectiva de los actores en los contextos de acción en los que los mismos se desempeñan; la misma resulta útil y de gran relevancia en nuestra investigación.

Asimismo, dicho trabajo de campo fue realizado en una escuela nacional dependiente de una universidad, la cual se ubica en un campus universitario. Esta institución cuenta con dos cursos por año de aproximadamente 35 estudiantes cada uno.
Se parte, por otro lado, de una definición amplia de “conocimiento escolar”; entendiendo como tal “el producto de un proceso de construcción colectiva que se expresa en las prácticas escolares cotidianas en el salón de clases” (Candela; 1995:176). Desde una perspectiva similar, Edwards sostiene que “los contenidos académicos son presentados en la escuela generalmente con carácter de verdaderos; en este sentido, se puede decir que transmiten visiones de mundo ‘autorizadas’” (Edwards; 1995:146). Estas conceptualizaciones acerca del conocimiento escolar y cómo éste es presentado en la escuela, nos permiten construir al espacio áulico como el ámbito escolar privilegiado en el cual se ponen en juego los procesos de apropiación de conocimientos científicos. ¿Qué dinámicas adquieren los mismos en las clases escolares? ¿Qué habilidades y saberes se privilegian y a cuáles se les da mayor importancia en este espacio? ¿Qué objetos median en los procesos de enseñanza-aprendizaje durante las clases? Estos interrogantes son relevantes a la hora de estructurar el análisis de procesos vinculados a la ciencia que se dan en ámbito áulico.

Si bien se sostiene que el aula es el espacio escolar más importante a la hora de indagar en los procesos de enseñanza-aprendizaje del saber científico; los estudiantes también participan de otros ámbitos en los que la ciencia ocupa un lugar central. Ejemplo de los mismos son las ferias de ciencias y las olimpíadas (de matemática, de filosofía, de biología, de física, etc.). Además de las clases escolares, los espacios concretos en los que también se busca indagar son los “talleres” de preparación de los estudiantes para su intervención en los certámenes de olimpíadas. En los mismos, ¿qué dinámicas adquieren los procesos apropiación de saberes científicos? ¿Qué habilidades y saberes se privilegian y a cuáles se les da mayor importancia en estos ámbitos? ¿Qué objetos median los procesos de enseñanza-aprendizaje durante esta clase de encuentros? Las preguntas planteadas aquí contribuyen a pensar en las diferencias entre los procesos que se dan en los talleres y aquellos que se desarrollan en el aula.

¿Por qué abordar, no sólo al ámbito áulico, sino también a las olimpíadas (y, específicamente, a los talleres en los que se prepara a los estudiantes para participar de ellas)? La respuesta a esta pregunta se relaciona con la posibilidad de indagar en las diferencias y las similitudes, las rupturas y las continuidades que pueden encontrarse en los procesos de apropiación de los saberes científicos en uno y otro espacio. Y, lo que es más relevante a esta investigación, tensionar las lógicas que se construyen en ambos espacios nos permite profundizar el estudio de las relaciones entre las concepciones que los estudiantes tienen sobre la ciencia y los modos en que los conocimientos científicos son presentados en los dos espacios educativos. Además, podríamos preguntarnos, ¿se desempeñan los actores de la misma manera y con los mismos criterios en uno y otro espacio?

A partir de las preguntas y distinciones conceptuales antes expuestas, se decidió trabajar con las clases y talleres de matemáticas. Por otra parte, debido a que existen varias clases de matemática en el establecimiento (a cargo de distintos docentes, con distintos alumnos y en distintos años); se decidió privilegiar el abordaje de aquellos ámbitos en los que sea posible la observación de los mismos actores en situaciones diferentes.

Las clases de matemática en Nacional
La dinámica general que se da en las clases de matemática en Nacional puede ser esquematizada a partir del siguiente gráfico:

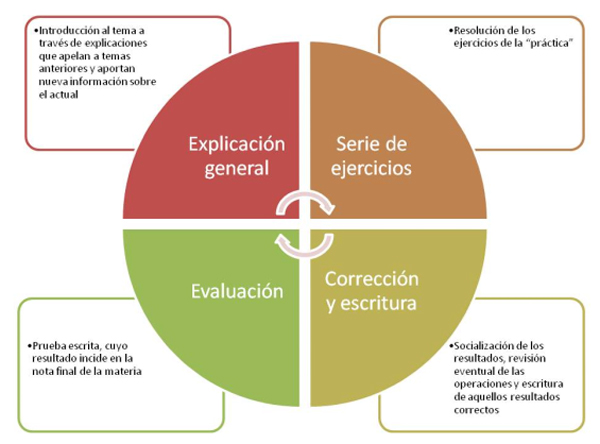
Cada encuentro se corresponde con uno o más de uno de los momentos que se cristalizan en el anterior esquema.
Cuando comienza a desarrollarse cada unidad temática, las explicaciones de la docente adquieren centralidad. En ellas, la misma intenta establecer relaciones entre los conceptos teóricos abordados en clases anteriores con aquellos que constituyen el eje principal en cuestión. Asimismo, la profesora va realizando preguntas a los estudiantes, a la vez que escribe ejercicios en la pizarra y solicita a los alumnos que le digan cómo los resolverían. En el proceso, aquella resuelve dudas, corrige las respuestas incorrectas y completa las que considera adecuadas, volviendo a explicarlas y dando más información al respecto.

Por otra parte, una cuestión de importancia consiste en que siempre está presente el conocimiento de la docente con respecto a qué “vieron” los estudiantes en años anteriores y qué “van a ver” en los posteriores. A su vez, también reviste suma relevancia el modo en que la profesora organiza la unidad temática y el esfuerzo que hace para ajustar las explicaciones a esta estructura; la cual constituye una progresión que va desde aquellos conceptos y formas más simples de resolver a los ejercicios más complicados.

Dadas las explicaciones generales durante las primeras clases en las que empieza a desarrollarse cada unidad temática, la dinámica de los siguientes encuentros en el aula gira en torno a dos momentos. Por un lado, la resolución (de forma individual o grupal) de los ejercicios de la “práctica”; y, por otro, la corrección de los mismos. Cuando se menciona la “práctica”, se está haciendo referencia al material elaborado por la docente que reúne la serie de ejercicios con los que los estudiantes trabajan a lo largo de las clases. Ésta complementa a la “teoría”[1], documento que recopila aquellos conceptos vertidos por la docente en cada explicación.

La mencionada resolución de los ejercicios suele realizarse grupalmente a pedido de la docente, quien marca qué puntos del práctico deben abordar los estudiantes. En general, la profesora da algunas sugerencias sobre cómo resolver y también orienta a los alumnos acerca de a qué prestarle atención (por ejemplo, la insistencia en “Quiero ver si ustedes pueden o podrían escribir las propiedades por ustedes mismos. La idea es ver si pueden identificar las propiedades”).
En este momento de la clase, mientras los estudiantes están realizando las tareas, las explicaciones de la docente no desaparecen. Por el contrario, si bien adquiere centralidad la labor de los primeros en rededor los ejercicios; la segunda es solicitada continuamente para que aclare dudas sobre la resolución. Ante éstas, la profesora da las explicaciones correspondientes a cada grupo que la llama, o bien llama la atención de todo el curso y explica para “todos”.
Se observa que la importancia de llegar al resultado correcto es, para los estudiantes, el objetivo a cumplir. En las consultas a la docente, por ejemplo, no le preguntan acerca de si el procedimiento realizado es correcto o no. Sólo se indaga en éste cuando el resultado no es el esperado. Por otra parte, comienza a visualizarse la dificultad de los alumnos para relacionar (y transcribir) las proposiciones en lenguaje matemático al coloquial (y viceversa).

Durante el paso de la docente por cada grupo que la solicita, la misma da explicaciones y aclaraciones sobre el tema y hace preguntas para que los estudiantes deduzcan las respuestas. “¿Cómo son las barras?”, “¿cómo son los números que están entre las barras? ¿Te das cuenta?”, “¿qué tipo de números nos da?”, por ejemplo. A su vez, insiste reiteradamente en la importancia de observar las propiedades e intentar “escribirlas” (es decir, enunciarlas).
En el momento de la corrección, no sólo se verifican los resultados obtenidos, sino que los procedimientos empleados adquieren también relevancia. En esta fase de la actividad áulica, a pedido de la docente, algunos estudiantes pasan a copiar en la pizarra aquello que hicieron en el grupo; debiendo el resto comparar ese trabajo con el propio. La profesora revisa paso por paso los procedimientos que permitieron llegar a los resultados esperados, corrigiendo oportunamente y explicando en caso de dudas o errores. En el proceso, hace preguntas a los estudiantes.

Sin embargo, a la hora de corregir los ejercicios, el protagonismo de la escena es acaparado por las “propiedades”. Como se afirmó anteriormente, la docente hace hincapié en todo momento en que los alumnos deben dar cuenta de las propiedades que les están permitiendo alcanzar la resolución del ejercicio. Y, a pesar de que las mismas están enunciadas en el apunte teórico (la “teoría”), ella insiste también en que los estudiantes intenten “ponerlas en palabras” y, además, que les quede escrita en sus carpetas. Esto último, también se repite con cada ejercicio corroborado en la socialización.
Puede decirse que los estudiantes deben establecer una triple relación entre: un ejercicio particular (“con números”), una proposición algebraica general y la enunciación de la propiedad (que corresponde, claro está, a la anterior). Aunque no siempre pueden vincular lo que está en la “teoría” y lo que hacen con los ejercicios de la “práctica”; llegando a confundirse el nombre de las propiedades y, en muchos casos, entendiendo su enunciación formal pero no pudiendo expresarlas por sí mismos.

El momento de la corrección es fundamental porque es cuando la docente va descartando ciertas formas de resolver los ejercicios. A este respecto, por ejemplo, en uno de los ejercicios, debe resolverse la ecuación: (x-3)2=4. Lo que la docente pretendía era que la misma fuese abordada a partir de los conocimientos vinculados al “valor absoluto de un número” (la unidad temática actual). Sin embargo, lo que uno de los alumnos planteaba era resolverla mediante la fórmula conocida como “bascara” (o fórmula de Bhaskara). De esta manera, la ecuación se iguala a 0 y se transforma en un polinomio de segundo grado plausible de ser resuelto con dicha fórmula. Éste era el “camino” conocido por los estudiantes. Pero no era el adecuado, debido a que se encontraba “fuera de contexto” (según la profesora). Esta vía “alternativa” puede ser, sin embargo, utilizada en la evaluación integradora porque ésta es, justamente, la instancia que “integra”, que “reúne” los contenidos del cuatrimestre. Sin embargo, si bien es un método lícito y válido, en el marco de la unidad correspondiente al “valor absoluto”; se espera que los alumnos resuelvan mediante los conceptos y los procedimientos a dicho tema asociados. Y son, en efecto, estos últimos los que se “consagran” a través de la escritura (para que les quede en el práctico).

Puede decirse, hasta aquí, que la organización de cada unidad temática tiende a la fragmentación de los conceptos y los procedimientos de resolución. Fragmentación que se desprende y se potencia con la distribución de los “contenidos” a partir de los diseños curriculares; los cuales, según las docentes entrevistadas, son acordados entre los profesores de cada año de la misma área. Es decir, los contenidos se coordinan entre dichos actores. Y, durante las clases (como se ha dejado entrever más arriba), la organización de los contenidos también está presente en el discurso de la docente.

Por otra parte, a diferencia de lo que ocurre en los talleres, la evaluación forma parte de la dinámica que se da en las clases. Ésta constituye el último momento que marcamos de dicha dinámica y, aún cuando no es próxima en el tiempo, representa una instancia que los estudiantes traen en todo momento a colación. Preguntan por cómo está siendo confeccionada, qué temas incluirá, si habrá ejercicios opcionales y demás interrogantes; los cuales la profesora no siempre contesta (porque aún no elaboró el examen o porque no “puede” hacerlo). Sin duda, las “evaluaciones integradoras” o simplemente “integradoras” (como le llaman en la escuela), constituyen el examen más desafiante para los alumnos; ya que se los pone a prueba respecto de todas las unidades temáticas “vistas” en el cuatrimestre. En el caso de las observadas, las mismas reúnen temas como sistemas de ecuaciones, resolución de ecuaciones cuadráticas y el valor absoluto.

Un elemento, que consignaremos como un “objeto”, que forma parte de la dinámica de las evaluaciones son las “cajas de herramientas”. Así denominan los actores (la docente y los estudiantes) al compendio de elementos que los alumnos pueden tener “sobre la mesa” al momento de los exámenes. Básicamente, los mismos pueden utilizar todo aquello que consideren necesario, salvo ejercicios resueltos. Sin embargo, a pesar de la insistencia de la profesora para que los estudiantes “preparen” o “armen” sus respectivas “cajas”, registramos que la gran mayoría no las preparó al momento de la prueba.
Anteriormente se sostuvo que los estudiantes se encuentran ante el imperativo de establecer una triple relación entre los elementos del conjunto formado por: ejercicios-enunciación algebraica-propiedades matemáticas. Dicho imperativo, en el contexto del examen, se vuelve vital para que aquellos puedan identificar (a partir de las consignas) cómo deben proceder y cuáles de los “elementos aprendidos” deben utilizar. Se afirmó, asimismo, que se observa cierta dificultad a la hora de llevar adelante estas asociaciones; a la vez que también se mencionó la importancia que adquieren los resultados en detrimento de los procedimientos desde el punto de vista de los alumnos. Todos estos rasgos que hacen a la apropiación del conocimiento se evidencian con mayor fuerza durante la evaluación.

Uno de los problemas que muestran los estudiantes se vincula con las fórmulas y su utilización en la resolución de un ejercicio. A este respecto, reemplazan mal los datos o no saben hasta dónde deben resolver, por ejemplo. En muchos casos, los mismos se equivocan en los pasos subsiguientes en el proceso de resolución. Estos identifican que hay un error, pero no pueden dar cuenta de qué se trata o en qué paso se encuentra. En dichos casos, la docente marca el procedimiento en el que se no operaron correctamente o los errores que cometieron en las cuentas. Otra cuestión fundamental está en la aplicación de las propiedades. Los estudiantes saben que las mismas están ahí y sirven para resolver, pero no identifican en qué circunstancias utilizarlas o cuándo hacer simplemente un “despeje de x”. Esto se suma al hecho que también llegan a aplicar mal las propiedades.

Otro problema fundamental para los alumnos se asocia a la respuesta que deben dar. En el caso de los sistemas de ecuaciones o las inecuaciones a partir del valor absoluto de un número, luego de hallar los posibles valores de “x”; estos deben presentarse en lo que se denomina “conjunto solución”. Sin embargo, durante la evaluación, los estudiantes parecen “olvidarse” de aquello o, directamente, no saber expresar de ese modo el “resultado” de sus procedimientos.

Como se ha mostrado a lo largo de este apartado, la capacidad que se requiere a los estudiantes es la de relacionar el conjunto conformado por: ejercicios-enunciación algebraica-propiedades matemáticas. La división en temas específicos, que hacen a cada unidad temática, se vincula a la compartimentación de los objetos de conocimiento que se vierten en el aula. El desarrollo de dichas unidades comienza con explicaciones generales a nivel conceptual, mostrando cómo la dinámica de las clases tiende a jerarquizar los conceptos teóricos sobre las posibilidades de resolución de situaciones problemáticas. De hecho, la triple relación de la que se habló anteriormente se orienta, no a la posibilidad de encontrar la solución (o soluciones) a un problema, sino a alcanzar el resultado correcto en un ejercicio. Esta distinción, entre problema y ejercicio, será fundamental para comprender (más adelante) las diferencias en el modo en que se construye el conocimiento en los talleres y en el aula. Mientras que los problemas requieren una lectura minuciosa y atenta, ponen en juego la capacidad de los actores para traducir los enunciados del lenguaje coloquial al matemático y no poseen un método de resolución evidente u obvia; los ejercicios presentan en su propia enunciación aquello que debe hacerse para encontrar el resultado.

La anterior diferenciación puede ilustrarse a partir de las consignas de la evaluación. En el caso de los ejercicios, por ejemplo, se lee: “Dada la ecuación x2+x-30=0 de raíces x1 y x2, calcular: x12-x22=” y “Resolver la ecuación y encontrar el conjunto solución: -2|x-5|+1=5-|-23|”. Para resolver estos ejercicios basta con identificar qué métodos utilizar: aplicar bascara, en el primero, y hacer la resta correspondiente con las raíces que arroja el cálculo; y, en el segundo, aplicar la propiedad multiplicativa y continuar luego resolviendo normalmente.

Por otro lado, en la evaluación se presentan los siguientes problemas: “La siguiente función determina la cantidad de pacientes que ingresan en un hospital después de x días que empieza una epidemia de gripe: p(x)=-x2+60x+700. ¿Cuál es el día en el que ingresan más pacientes? ¿Cuál es la cantidad máxima de pacientes que ingresaron durante la epidemia? ¿Cuánto dura la epidemia?” y “El número de personas atacadas cada día por una determinada enfermedad viene dada por la función: p(x)=-x2+40+84, donde x representa el número de días transcurridos desde que se descubrió la enfermedad. (…) ¿Cuál es el número máximo de personas atacadas por la enfermedad? ¿Cuándo deja de crecer el número de personas afectadas por la enfermedad? ¿Después de cuántos días no quedarán personas enfermas?”.

En los últimos ejemplos de problemas, en cambio, la solución no se desprende de la lectura superficial del enunciado. El estudiante que se posiciona frente a los mismos debe ser capaz de identificar qué es lo que tiene que hacer y, encontrados los posibles métodos de resolución, dar cuenta de qué significan los resultados obtenidos. No se agota, entonces, la cuestión aplicando una fórmula, utilizando las propiedades “vistas” o resolviendo analíticamente.

Sin embargo, mientras que los ejercicios responden a la mayor parte de los elementos dados en la “práctica” y son obligatorios en la evaluación; los problemas corresponden a los elementos menos frecuentes en los trabajos prácticos y son de resolución opcional (para “levantar” la nota). Además, los mismos son los que, en clase, más les ha costado resolver a los estudiantes.

Esta distinción entre ejercicios y problemas, sumada a la reconstrucción que se ha hecho hasta aquí de la dinámica de las clases y su relación con las capacidades que se jerarquizan en el aula; constituyen los rasgos centrales que hacen a los procesos de apropiación del conocimiento científico en las clases escolares.

Reduciendo[2] el taller de matemáticas
El taller está coordinado por dos docentes (A. y Z.), una de las cuales es la misma cuyas clases observamos (Z.), y tres estudiantes (R., N. y O.). La dinámica del mismo puede esquematizarse a través del siguiente gráfico:

En un primer momento de la actividad, los estudiantes se dedican a resolver los problemas contenidos en los cuadernos de OMA[3] y Ñandú[4]; o, en su defecto, trabajan sobre problemas utilizados en ediciones anteriores de la respectiva olimpíada. Los objetos se constituyen en ejes vertebradores del trabajo de preparación para la competencia. Sin embargo, puede hacerse una distinción fundamental entre unos y otros elementos dentro del circuito de la OMA[e]: 1) los ejercicios utilizados en ediciones anteriores del certamen, así como otros que están disponibles para su descarga o bien son enviados por correo electrónico a través de una lista de correos en la que el interesado debe sumarse, son gratuitos; por otro lado; 2) los cuadernos, así como los libros de corte teórico, deben comprarse. A diferencia de los “problemas descargables”, los cuadernos de la OMA contienen tanto los ejercicios como sus soluciones; varias de ellas extraídas directamente de las respuestas de estudiantes frente a esos problemas en evaluaciones de años anteriores. Por otra parte, la organización de ambos objetos se construye a partir de las categorías de participación que define la OMA; es decir, los tres niveles en que los alumnos pueden participar. Asimismo, en el caso de los cuadernos (los elementos más utilizados durante el taller), sólo contienen los enunciados y sus resoluciones; pero no traen explicaciones ni análisis teóricos sobre las bases conceptuales de los problemas presentados.

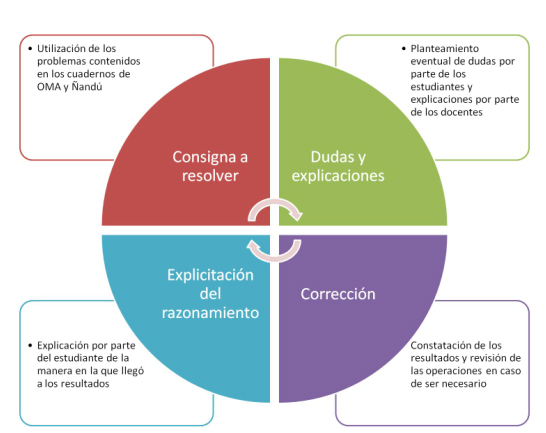
Por otro lado, los estudiantes no realizan cualquier ejercicio dentro de todos los que contienen los cuadernos. Para el caso de R. y N., A. parece indicar de qué sección del libro deben extraer los enunciados sobre los cuales trabajar. A partir de esto, los alumnos tienen cierto margen de libertad para seleccionar qué hacen y qué no; aunque la docente presta atención a que los mismos realizan todos los tipos de ejercicios (de geometría, de conteo, etc.).

En el segundo momento de la actividad, los estudiantes plantean dudas y hacen preguntas, las cuales son contestadas por las docentes a partir de las explicaciones correspondientes. Las mismas son siempre “prácticas”. Con esto nos referimos a que, en general, las profesoras intentan “dar pistas” a los estudiantes sobre cómo resolver los problemas abordados. Sólo se dedican a “explicar un tema” (conjunto de conceptos teóricos generales relacionados) en caso de ser necesario, pero siempre esta explicación está relacionada a la resolución de un enunciado. Por otra parte, el tercer momento remite a la corrección de los ejercicios; es decir, a la revisión de los resultados y, de ser necesario ante posibles errores, de las operaciones realizadas. Ambos momentos no siempre se dan de manera lineal (primero uno, luego el otro), sino que a menudo se superponen o hasta constituyen un mismo proceso dentro la resolución de los problemas. Una de las cuestiones más interesantes en este punto consiste en que, a la hora del planteamiento de dudas o la formulación de aclaraciones y explicaciones sobre los ejercicios, los roles típicos de los estudiantes y las docentes se conmutan. Esto es, en ocasiones los propios estudiantes explican a sus pares y los docentes requieren la opinión de los alumnos sobre tal o cual enunciado.
Asimismo, la rapidez en el hallazgo de las maneras de resolver parece ser una variable altamente valorada por los estudiantes.

O se convierte, en diferentes momentos del taller, en el foco de atención. Este estudiante, el de mayor edad y el más elogiado por las docentes, parece transformarse  en una muestra del conjunto de facultades que se deberían alcanzar. Podría pensarse, incluso, en que O. se transforma en una suerte de “referente” para sus pares. Sin embargo, lo interesante aquí es preguntarse cómo se da esto, ¿se relaciona con una actitud propia del estudiante mayor o más bien remite al conjunto de afirmaciones y explicitaciones sobre este alumno que hacen las docentes? Claramente, la respuesta se orientaría hacia el segundo eje de este interrogante.

Ahora bien, el cuarto momento del esquema con que hemos graficado (y, claro está, simplificado) la dinámica del taller se refiere a la “explicitación del razonamiento”. Con esto nos referimos al hecho de dar cuenta de cómo los estudiantes “pensaron” los ejercicios; es decir, de cómo llegaron a sus resultados. Este punto resulta nodal en el desarrollo del encuentro y parece constituirse como la piedra angular en el entrenamiento de los alumnos. El modo en que se piensan los ejercicios parece constituirse en la piedra angular del saber hacer del que se apropian los estudiantes.

Sostenemos que la explicitación de los razonamientos es la pieza fundamental del entrenamiento de los estudiantes y, además, se constituye en la habilidad clave de la distinción de O. entre el “resto”. Es decir, este estudiante es “especial” (desde el punto de vista de los actores) porque poseería una facultad que otros no tienen, porque puede hacer las cosas de una manera que a otros “les cuesta más”. Y, lo que más parece asombrar a los participantes del taller, es que esta habilidad de O. aparece como “innata”; nadie le enseñó a pensar así, nadie le enseñó a resolver de esa manera los ejercicios. ¿Tiene O. un inherente don para las matemáticas? ¿Es un “prodigio”?

No puede dejar de sorprender que un estudiante de primer año de secundaria realice ejercicios preparados para alumnos, al menos, un año mayores que él y que, además, comprenda con una inusitada rapidez temas “nuevos”. Aunque, de ahí a considerarlo poseedor de una facultad extraordinaria hay, en efecto, una distancia abismal. Entonces, evocando nuevamente los interrogantes antes mencionados, ¿tiene O. un inherente don para las matemáticas? ¿Es un prodigio? Nuestra respuesta no es necesariamente negativa (ya que no podríamos ni nos interesa evaluar la excepcionalidad intelectual de nadie); sino que se construye (y aquí sí, necesariamente) a partir de otros elementos. Anteriormente, identificamos a la capacidad para explicitar los razonamientos a partir de los cuales se llega a la resolución de un problema matemático (es decir, a la capacidad de poner esos razonamientos en palabras de manera fluida y de dar cuenta de ellos de manera escrita) como el centro de la diana al que apunta la formación o, si se quiere mencionar de otra manera, la preparación de estos estudiantes para su participación en las olimpíadas. Esta capacidad de explicitación del razonamiento no tiene que ver, al menos en este punto y al nivel en que lo estamos analizando, con el aprendizaje de conceptos teóricos o con el dominio de un tipo particular de método matemático. Casi por el contrario, se trata de un saber hacer. En otras palabras, puede hablarse aquí de un sentido práctico. “Sentido práctico” en un sentido muy similar al que se refiere Bourdieu en términos de aquellas racionalidades prácticas de los sujetos que se construyen en función de sus esquemas de acción y de percepción; y que, además, atienden a las condiciones específicas en que se elaboran (Bourdieu; 2007).

La teoría de la práctica de Bourdieu nos habla de que los objetos de conocimiento son construidos a partir del sistema de disposiciones que se constituye en la práctica y que siempre están orientadas hacia la práctica. Este conjunto de disposiciones es, justamente, lo que el autor denomina habitus: “Los condicionamientos asociados a una clase particular de condiciones de existencia producen habitus, sistemas de disposiciones duraderas y transferibles, estructuras estructuradas predispuestas a funcionar como estructuras estructurantes, es decir, como principios generadores y organizadores de prácticas y de representaciones” (Bourdieu; 2007:86).

Por otro lado, el hecho de naturalizar la diferencia (por parte de las docentes) entre “todos los demás estudiantes” y “estos estudiantes” (los que tienen un interés y una habilidad “innata” para las matemáticas), y aún entre todos estos una suerte de “prodigio” entre los “ya aventajados”; forma parte del acto de institución (Bourdieu; 2007) de estas diferencias.

Hasta aquí se dio cuenta de las instancias clave en el desarrollo de los talleres de matemática de Nacional. Por otro lado, se puso en evidencia, dentro de los cuatro momentos que diferenciamos, aquel que es considerado (desde la perspectiva de los actores) como el más importante: la explicitación del razonamiento a través del cual los alumnos llegan a las soluciones de los problemas. Ahora bien, ¿por qué esta instancia es tan importante? ¿Cómo son los problemas que propone la OMA? ¿Son utilizados en clase? ¿En qué aspectos se diferencia la actividad del taller con respecto al desarrollo de una clase de matemáticas en el marco del currículo escolar? ¿En qué marcos se construye ese saber hacer que distingue a los estudiantes que participan de las olimpíadas de matemáticas y, entre ellos, a O. en particular? ¿Qué operaciones por parte de qué actores permiten la construcción de un “genio”?

En principio, como marcamos en anteriores apartados, el primer punto de inflexión en la distinción entre las clases y los talleres, consiste en el predominio en la utilización de ejercicios o problemas (respectivamente); atendiendo a la diferenciación que hicimos más arriba entre ellos.

Además, según las docentes, la cantidad de estudiantes, la motivación de cada uno de ellos con respecto a la materia en cuestión y los contenidos en juego son las cuestiones centrales que pueden observarse como rupturas en la diferenciación entre la actividad áulica y aquella que se da en el taller. En este último espacio, el número de alumnos que concurre es notablemente menor que el de aquellos que asisten a clases. Esto permite, por otro lado, un trabajo personalizado que, según las docentes, no es posible sostener en las clases escolares. Sin embargo, el punto clave de ruptura parece ser la motivación de los estudiantes. “[...] el interés. Ya ahí es el punto de partida. [Los estudiantes que asisten al taller] Están más motivados. Ya eso es una cosa que para nosotros es el 50% ganado. Porque los chicos están motivados, les gusta hacer esto. Y en el aula vos tenés de todo”.

Por otra parte, los contenidos en juego en los procesos de enseñanza-aprendizaje que se dan en el aula como aquellos que se dan en el espacio del taller, constituyen otro punto de ruptura entre el desarrollo de la actividad en una y otra instancia. Esto se relaciona con el hecho que los problemas con que se trabaja en las olimpíadas “[…] no entran en un único contenido de los que vos ves, de lo que desarrollás en clase”, según afirma una de las docentes. Los estudiantes deben aprehender conocimientos que muchas veces van más allá de lo “esperado” (según la lectura que se hace de los diseños curriculares); es decir, de lo que “deberían saber” según el año en el que están en la escuela. Incluso, los actores entrevistados dan cuenta que, directamente, muchos de los conocimientos que requieren los alumnos van más allá de lo que estos podrían aprender en la escuela. Además, puede observarse también que la progresión en el aprendizaje de los contenidos parece resultar mucho más veloz en el espacio del taller que en el del aula. ¿Por qué se dan estas diferencias entre la dinámica de uno y otro espacio? ¿Qué diferencia los procesos de apropiación de los conocimientos que se dan en el taller con respecto a aquellos se dan en el aula? ¿Por qué un estudiante puede, en el taller, aprender de manera más rápida que en la clase escolar?

Para responder los interrogantes anteriores, es necesario volver a poner en escena a los problemas con que se trabaja en los talleres. Para su resolución, se requiere de la utilización de variados conocimientos, de la puesta en práctica de diferentes métodos y la aplicación de propiedades diversas. La clave se encuentra en el hecho que, si bien muchos de estos conocimientos, métodos y propiedades forman parte de los temas trabajados en el aula escolar; las prácticas que se desarrollan en el marco de las olimpíadas requieren su integración. Es decir, mientras que en la escuela los temas se dan “por separado”; en las olimpíadas se vuelve necesario combinar dichos temas. Aquí se encuentra el punto clave en la diferenciación entre el desarrollo de una clase escolar y el desarrollo de un taller en el marco de las olimpíadas de matemática. Mientras que la primera instancia el objetivo central consiste en que los estudiantes “aprendan” o “sepan” un determinado “tema”; el fin de la segunda se orienta a que los mismos sean capaces de “resolver” situaciones problemáticas.
En un estudio anterior (Medici; 2012), se mostraba cómo los diseños curriculares pueden ser caracterizados a través de la combinación de dos propiedades: son organizadores de la malla curricular y ofrecen un “enfoque”. De estas dos propiedades, la que aquí nos interesa es la primera; la cual remite a que dichos diseños. La dinámica de una clase escolar parte, si se permite la esquematización, de los diseños. Estos indican, en lo que a este respecto nos incumbe, los contenidos que deben darse en cada materia y en qué año se espera que estos contenidos sean aprehendidos; en otras palabras, podríamos decir que “compartimentan” los saberes específicos de cada disciplina. Los conceptos teóricos ocupan el primer plano de la escena en el aula. Por su parte, los ejercicios, referentes a las formas en que se debe proceder en tal o cual caso, quedan relegados a un lugar secundario (claro que pensando en problemas y no en simples ejercicios).

¿Por qué se dan estas diferencias? ¿Por qué, a pesar de que en las clases escolares se pone en primer plano los conocimientos teóricos (propiedades de tal o cual operación, por ejemplo), los alumnos parecen no ser capaces de utilizar dichos conocimientos para resolver problemas? ¿Por qué los estudiantes que asisten al taller sí pueden hacerlo?

La cuestión nodal reside en el desarrollo del taller. Aquí, los imperativos de los diseños se mantienen por fuera de la actividad. En su lugar, los cuadernos de OMA son los objetos (o cuasi-objetos) que organizan la actividad. Sin embargo, en vez de clasificar y ordenar “temas”, estos proponen problemas y legitiman ciertos modos de resolverlos[6]. Las situaciones problemáticas pasan al primer plano de la escena. Lo que se da, en realidad, es una inversión de la jerarquía construida al interior del aula. La pregunta cómo resuelvo adquiere aquí mayor preponderancia que la pregunta qué debo saber.

Los conceptos teóricos son parte esencial en el desarrollo de las mencionadas situaciones problemáticas. Sin embargo, el modo de presentarlos en el espacio del taller, subordinados a la resolución del problema, permite entender por qué estos estudiantes logran lo que los alumnos en las clases no alcanzan. En el taller, los procesos de apropiación del conocimiento están atravesados por una tendencia hacia las formas de abordar problemas y encontrar las vías para resolverlos. Y, debido a la complejidad pero también a que desde su concepción dichos problemas poseen esta orientación eminentemente “práctica”, es que los alumnos que participan de las olimpíadas pueden “integrar” los conocimientos teóricos.

Hasta aquí hemos puesto en tensión las relaciones entre la clase escolar y el taller de matemáticas; con el fin de mostrar cómo este último se constituye en el marco que permite, a los estudiantes que se preparan para participar de las olimpíadas de matemáticas, construir un saber hacer particular. “Saber hacer” enunciado en tanto sentido práctico; ya que el mismo consiste en el conocimiento de las reglas específicas de un juego también específico, de los modos de hacer y resolver ciertas situaciones, de las formas de desenvolverse en un determinado terreno. Hablamos de sentido práctico, justamente, porque se trata de la construcción de un conjunto de disposiciones que permiten que los actores entiendan cómo tienen que moverse y en qué dirección orientar sus estrategias de acción; en este caso en particular, dentro de las olimpíadas.

Consideraciones finales
El trabajo realizado en Nacional ha permitido evidenciar la manera en que el desarrollo de las actividades vinculadas a las clases escolares y los talleres de olimpíadas se diferencian entre sí; al punto de perseguir objetivos y alcanzar resultados indefectiblemente relacionados, pero concretamente distintos. De un lado, una lógica que orienta la actividad (dentro de la clase) a la adquisición de conceptos abstractos (o abstraídos), basada en las prescripciones y los imperativos de los diseños curriculares. Del otro, la construcción de un espacio cuya lógica subordina aquellos conceptos al aprendizaje de formas creativas, muchas veces intuitivas y complejas para resolver situaciones problemáticas; y sostenido en base al entrenamiento en la resolución de estos problemas, que requieren la integración de aquello que en el aula se compartimenta. Y, lo más relevante e interesante desde nuestra perspectiva, es que el desarrollo de ambos espacios es construido por los mismos actores que día a día conforman la cotidianidad del aula y del taller. Por otra parte, en este escenario, la figura de O. nos ha permitido relevar otro hito fundamental en lo que respecta al desarrollo del taller, en particular, y de las olimpíadas, en general: se trata de la construcción de un saber hacer. Un saber hacer propio y específico del contexto en el que éste se construye (el taller) y al cual está orientado (las instancias de evaluación de la olimpíada); y que antes hemos denominado también como “sentido práctico”, ya que implica un sentido de las “reglas del juego” y un ajuste de las acciones del sujeto según su posición “en el tablero”. Asimismo, hemos relacionado estas nociones con el concepto de habitus de Bourdieu. Sin embargo, dicho concepto se topa con necesarios obstáculos a la hora de leer nuestro problema de estudio desde una perspectiva más integral, considerando todos los elementos y las dimensiones que hemos seleccionado para su análisis.

El sociólogo francés Bernard Lahire explica que, a diferencia de lo que puede entenderse a partir de los conceptos de campo y habitus (Lahire; 2011), el mundo social en el que se desenvuelven los individuos da cuenta de un sin número de “experiencias socializadoras”; las cuales son heterogéneas y hasta contradictorias entre sí (Lahire, 2011). “esto quiere decir que no tenemos incorporado un sistema coherente y homogéneo de disposiciones que puede transferirse para todos lados, sino que somos el producto de disposiciones heterogéneas y muchas veces contradictorias” (Lahire; 2011:72), sostiene el autor. De este modo, estas “disposiciones heterogéneas” van a inhibirse/suspenderse o a activarse según la situación en la que se encuentre el sujeto. Esto es lo que hace que Lahire se refiera a un “actor plural”. Estas nociones del autor apuntan a poner en jaque a los conceptos de campo y habitus de Bourdieu, focalizándose en varios de los elementos que corresponden a cada uno de estos términos (sobre todo al primero)[7]. Sin embargo, lo que aquí nos interesa es la crítica a la coherencia u homogeneidad del habitus, a la vez que su supuesto carácter transferible, durable y generalizable.

Por otro lado, Lahire afirma también que “deducir apresuradamente del análisis de las prácticas de un individuo, o de un grupo social, en un contexto social determinado (cualquiera que sea la escala del contexto), esquemas o disposiciones generales, habitus que funcionarían de la misma manera en cualquier lugar, en otros lugares y en otras circunstancias, constituye un error de interpretación” (Lahire; 2005:24)[8]. De esto se deduce que, además de la homogeneidad en la que está imbuido el concepto de habitus, la transferibilidad del mismo se constituye en obstáculo para comprender cómo, en un mundo pleno de experiencias socializadoras heterogéneas, los esquemas de acción que posee un actor pueden transferirse de un contexto a otro.

Estas reflexiones conceptuales, no apuntan a desechar las contribuciones que el concepto de habitus puede aportar a la lectura de nuestro problema de investigación, sino a pensar en el “saber hacer” o “sentido práctico” que antes hemos planteado desde otra perspectiva. Considerar lo que Lahire denomina “patrimonio de disposiciones” (Lahire; 2005) en vez de lo que Bourdieu llama habitus (Bourdieu; 2007), nos permite entender a nivel teórico el hecho que, los mismos individuos, sean actores de obras que se desarrollan de manera completamente diferente (aún cuando de ninguna manera se niegan las relaciones entre ellas).

Finalmente, desde la perspectiva que propone Lahire, resulta comprensible que las mismas profesoras que se desempeñan tanto en el aula escolar como el taller de matemáticas orienten los procesos de enseñanza-aprendizaje hacia objetivos diferentes y de modos también diferentes en una y otra de estas situaciones. Asimismo, se vuelve más transparente la construcción por parte de los estudiantes (pero también, en diferente grado, de las docentes) de un sentido práctico que se define diametralmente distinto a aquellas lógicas de acción esperables y promovidas en el aula. De la misma manera, encuentra sentido la manera en que O. se destaca del resto a partir de sus “capacidades”; es decir, de un saber hacer finamente construido a lo largo de su trayectoria vital, y construido en diferentes espacios sociales, como aquellos vinculados a la escuela.

Por otra parte, los esquemas que hemos construido para diferenciar el desarrollo de la clase escolar de la dinámica del taller y mostrar, de esta manera, el modo en que ambos marcos moldean diferentes sentidos del hacer y del saber; permite retomar la discusión acerca de las relaciones entre las nociones de ciencia que construyen los estudiantes en la escuela (Medici; 2012) y los procesos de apropiación de conocimientos científicos que se desarrollan en contextos escolares diferentes. En principio, es necesario decir que no es posible construir un vínculo directo (al modo de relación causa-efecto) entre un punto y otro de dichas relaciones. Sin embargo, el análisis realizado hasta aquí sí permite importantes reflexiones a este respecto.

Como antes explicamos, desde nuestra perspectiva, los “diseños” poseen dos características: son organizadores de la malla curricular y proponen un enfoque. Desde lo organizacional (y tomando en este punto solamente aquello que nos interesa para graficar la cuestión), dichos diseños generan una grilla de espacios curriculares y prescriben aquello que debe “darse” en cada uno a partir de “contenidos” y “temas”; los cuales son retomados (y reelaborados) en las clases. Esta sucesión de instancias (groseramente simplificadas para facilitar la comprensión de nuestro punto de vista), se encuentra atravesada por dos cuestiones. La primera se refiere a las nociones que vuelcan los diseños a través de su enfoque (Medici; 2012); las cuales tienden hacia la desnaturalización de los principios positivistas de la ciencia (universalidad, objetividad, neutralidad valorativa, etc.) que, como mostramos en un estudio anterior (Medici; 2012), dista enormemente de las concepciones de ciencia que construyen los estudiantes. Por otro lado, se produce una compartimentación de los contenidos; orientando, además, los procesos de enseñanza-aprendizaje hacia la aprehensión de conceptos abstractos. En cambio, los talleres de olimpíadas están atravesados por la presentación de situaciones problemáticas; las cuales tienden hacia la apropiación de modos de resolver las mismas por caminos múltiples y complejos. Asimismo, para que sea posible encontrar respuestas a las indagaciones planteadas por los certámenes abordados, se requiere una integración de todos los conocimientos adquiridos. Integración que difiere, si no se opone, a aquella compartimentación de los saberes que se escurre por los circuitos áulicos.
En ambas situaciones, la presentación de los saberes científicos y los procesos de apropiación de los mismos se encuentran aún lejos de orientarse hacia una desnaturalización de la ciencia y un abordaje que la observe como una actividad humana socialmente construida; y no como una institución fría, inmutable y poseedora cuasi absoluta de los criterios y métodos para acceder a la “Verdad”. Sin embargo, lo que nos demuestran las experiencias desarrolladas en los talleres de olimpíadas, es que es posible (y, de hecho, ocurre) construir modos de aproximarse a la ciencia que sean diferentes a aquellos que se dan generalmente en el espacio áulico.

1. Práctica y teoría son los términos nativos con los que los actores denominan a los documentos descriptos. Volver al texto

2. Jugamos con la definición matemática del término “reducción”, nombre con el que se conoce uno de los métodos para resolver sistemas de ecuaciones. Volver al texto

5. Salvo se indique lo contrario, el término “OMA” se usará para referirse a ambas olimpíadas (la OMA propiamente dicha y la OMÑA). Volver al texto

6. Ya que estos cuadernos traen posibles soluciones a los problemas; muchas de las cuales fueron elaboradas por participantes de las olimpíadas durante la competición. Volver al texto

Bourdieu, P. (2007). El sentido práctico. Buenos Aires: Siglo XXI.
Candela, A. (1995). Transformaciones del conocimiento científico en el aula. En: Rockwell, E. (coord.). La escuela cotidiana. México: Fondo de Cultura Económica.
Edwards, V. (1995). Las formas del conocimiento en el aula. En: Rockwell, E. (coord.). La escuela cotidiana. México: Fondo de Cultura Económica.
Guber, R. (2001). La etnografía: método, campo y reflexividad. Bogotá: Grupo Editorial Norma.
Lahire, B. (1998). El hombre plural: los resortes de la acción. Barcelona: Edit. Bellaterra.
Lahire, B. (2002). Campo, fuera de campo, contracampo. Colección Pedagógica Universitaria, no. 37-38 (enero-junio / julio-diciembre), p. 1-37.
Lahire, B. (2005). Patrimónios individuais de disposiçiões: Para uma sociologia à escala individual. En: Sociologia, problemas y prácticas. No. 49, p. 11-42. Las traducciones de los fragmentos transcriptos son nuestras.
Lahire, B. (2011). Socializaciones y disposiciones heterogéneas: sus vínculos con la educación. Entrevista realizada por Victoria Gessaghi y María Alejandra Sendón. Propuesta Educativa, n° 30, p. 71-77.
Medici, E. N. (2012) “Ciencia y escuela: reflexiones en torno a la construcción de sentidos sobre el saber científico en estudiantes del nivel medio de enseñanza”. En: Revista Argentina de Humanidades y Ciencias Sociales, ISSN 1669-1555, vol. 10, no. 2.